一、 Overview

The Rotational Viscometer (RV) (Figure 207 and Figure 2) is used to determine the viscosity of asphalt binders in the high temperature range of manufacturing and construction. This measurement is used in the Superpave PG asphalt binder specification. The RV test can be conducted at various temperatures, but since manufacturing and construction temperatures are fairly similar regardless of the environment, the test for Superpave PG asphalt binder specification is always conducted at 275°F (135°C).

The RV test helps ensure that the asphalt binder is sufficiently fluid for pumping and mixing (Roberts et al., 1996[1]).

The basic RV test measures the torque required to maintain a constant rotational speed (20 RPM) of a cylindrical spindle while submerged in an asphalt binder at a constant temperature. This torque is then converted to a viscosity and displayed automatically by the RV.

The standard Rotational Viscometer procedure is found in:

•  AASHTO T 316 and ASTM D 4402: Viscosity Determination of Asphalt Binder Using Rotational Viscometer.

二、 Background

The viscosity of asphalt binder at high manufacturing and construction temperatures (generally above 275°F (135°C)) is important because it can control the following:

•  Pumpability. The ability of the asphalt binder to be pumped between storage facilities and into the HMA manufacturing plant.
•  Mixability. The ability of the asphalt binder to be properly mixed with and to coat aggregate and other HMA constituents in the HMA manufacturing plant.
•  Workability. The ability of the resultant HMA to be placed and compacted with reasonable effort.

The RV (Figure 208) gives a rapid and reproducible measurement of high temperature viscosity which correlates closely with the more traditional, but time-consuming, glass capillary viscometer method.

About the RV

The rotational viscometer senses torque required to rotate a spindle at constant speed while immersed in the sample fluid. Dynamic viscosity is proportional to this measured torque.

The standard RV is quite common in chemical and food industries for measuring the viscosity of non-Newtonian fluids. Typical uses include:

•  characterization of margarine and table spread melting
•  candy coating viscosities
•  mixing and storage stability of paints
•  food formulation quality control checks
•  characterizing sol to gel transitions in gelatins

The RV vs. Other Viscosity Methods

There are several different methods typically used for measuring viscosity besides the RV. Each one has appropriate uses but each also has significant weaknesses when applied to asphalt binder:

•  Ford cup (Figure 4).Measures the time that a defined sample volume needs to flow through a nozzle.
• ○ Disadvantages: No temperature control, does not work for non-Newtonian fluids.
•  Falling ball (Figure 5). Measures the time that the ball needs to fall through a distance of 3.93 inches (100 mm) in a tube of 10° inclination.
• ○ Disadvantages: Application limited to thin, transparent Newtonian fluids.
•  Capillary viscometer (Figure 209). Measures the time for a sample to flow through a small tube either under a controlled head or vacuum.
• ○ Disadvantages: Takes long to run and modified asphalt binders (especially those containing crumb rubber) may become clogged in the tube.
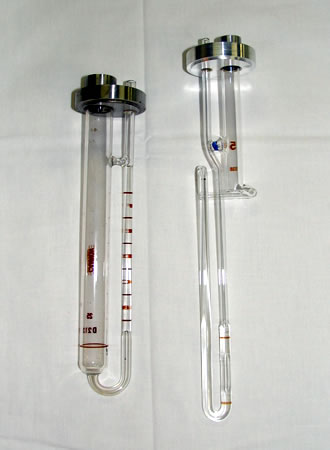Figure 209:Capilary viscometer tubes.

The RV provides for a wide range of temperatures, works with non-Newtonian fluids (like asphalt binder), works for opaque fluids, is relatively quick, and works for modified asphalt binders. Therefore, the Superpave PG asphalt binder specification uses the RV for high temperature viscosity measurement.

三、 Test Description

The following description is a brief summary of the test. It is not a complete procedure and should not be used to perform the test. The complete procedure can be found in:

•  AASHTO T 316 and ASTM D 4402: Viscosity Determination of Asphalt Binder Using Rotational Viscometer.

Summary

The basic RV test measures the torque required to maintain a constant rotational speed (20 RPM) of a cylindrical spindle while submerged in an asphalt binder at a constant temperature (typically 275°F (135°C)). This torque is converted to a dynamic viscosity and displayed automatically by the RV. Figure 210 shows the major equipment involved.

Approximate Test Time

1.5 hours from sample preparation to final viscosity reading for one temperature. 2.5 hours for two temperatures.

Basic Procedure

1. 1. Preheat spindle, sample chamber, and viscometer environmental chamber (Thermosel) to 275°F (135°C).
2. 2. Heat unaged asphalt binder until fluid enough to pour. Stir the sample, being careful not to entrap air bubbles.

Heating time should be minimized to avoid oxidative hardening and volatile loss that will further harden the sample. (AASHTO, 2000c).

3. 3. Pour appropriate amount of asphalt binder into sample chamber (Figure 211). The sample size varies according to the selected spindle (Figure 212) and equipment manufacturer.
Figure 211: Pouring a RV sample into the sample chamber.
Figure 212: RV sample chambers and spindles.
4. 4. Insert sample chamber into RV temperature controller unit and carefully lower spindle into sample (Video 27).
Video 27: Inserting the sample into the temperature controller unit.
5. 5. Bring sample to the desired test temperature (typically 275°F (135°C)) within approximately 30 minutes and allow it to equilibrate at test temperature for 10 minutes.
6. 6. Rotate spindle at 20 RPM, making sure the percent torque as indicated by the RV readout remains between 2 and 98 percent (Video 28).
Video 28: RV rotating at 20 rpm.
7. 7. Once the sample has reached temperature and equilibrated, take 3 viscosity readings from RV display, allowing 1 minute between each reading. Viscosity is reported as the average of 3 readings.

四、 Results

Parameter Measured

Dynamic (or absolute) viscosity.

Specifications

Table 20: Performance Graded Asphalt Binder RV Specification

Material	Value	Specification	Property of Concern
Unaged binder	Dynamic viscosity	≤ 3 Pa•s	Pumping, mixing and workability

Typical Values

RV viscosities depend upon the material measured and the test temperature. Superpave testing is done at 275°F (135°C) and typical dynamic viscosity values for asphalt binders at this temperature are 0.2 to 2 Pa·s. The Asphalt Institute recommends using a value of about 0.28 Pa·s for compaction temperatures. At high in-service pavement temperatures (e.g. on a hot summer day of 140°F (60°C)) dynamic viscosity can be around 200 Pa·s. Some representative dynamic viscosities are:

•  PG 64-22 asphalt binder at 275°F (135°C) ≈ 0.570 Pa·s
•  PG 76-22 asphalt binder at 275°F (135°C) ≈ 1.800 Pa·s
•  Water at room temperature = 0.001 Pa·s
•  SAE 10 oil at room temperature = 0.088 Pa·s
•  Liquid Honey at room temperature = 2 Pa·s
•  Mayonnaise at room temperature = 5 Pa·s

Calculations (see Interactive equation)

Most RVs provide a viscosity readout in centipoise (cP) or Pascal-seconds; the operator is not required to make any complex calculations. At most, the operator may have to covert cP to Pa·s using:

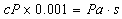
The basic equations used to calculate viscosity from torque and speed (expressed in terms of angular speed) are:

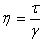
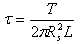
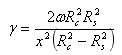
Where:

• η = dynamic viscosity (Pa·s)
• τ = shear stress (N/cm2)
• γ = shear rate (sec-1)
• T = torque (in N·m)
• L = effective spindle length (m)
• Rs = spindle radius (m)
• Rc = container radius (m)
• ω = rotational speed (radians/second)
• x = radial location where shear rate is being calculated (m)

Typically, the RV simplifies this calculation by measuring torque in percent (0 to 100), dividing it by RPM and then multiplying it by a series of constants determined by the spindle used. This procedure is what the interactive equation shows.